Articles

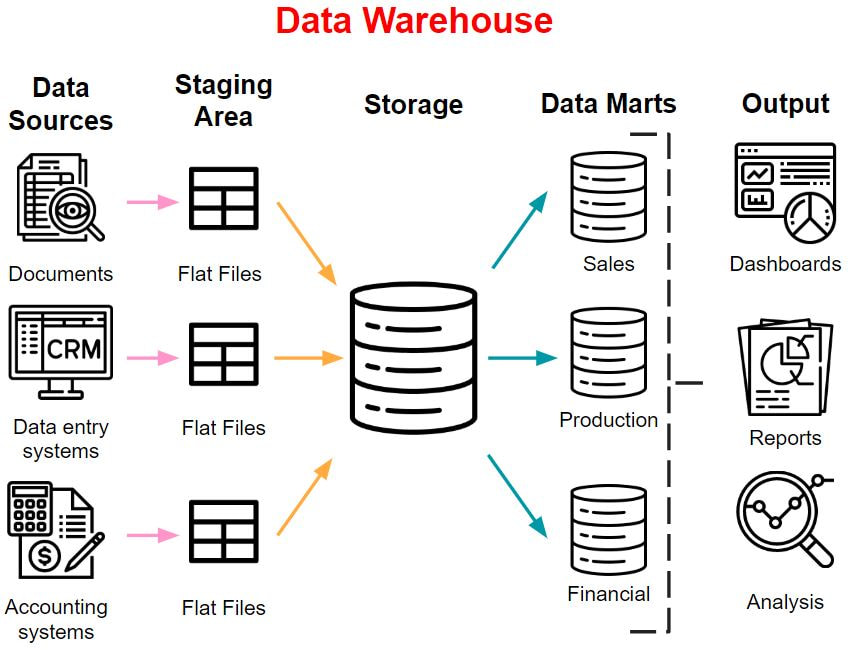
24/2/2020 5 Comments

data warehousing

Overview

Unlike many misleading tech pseudonyms (looking at you ‘growth hacking’), data warehousing is a really good name:

Warehouse: a building that collects materials, stores and packages them in a sensible order and sends the materials off to other parts of the business when required
Data warehouse: a computer system that collects, stores, processes and outputs data

Although data warehousing sounds technical (and possibly complicated), if you have ever built a spreadsheet that records data in a sensible order, you have made a simple data warehouse.

However, modern day business information is vast, complex and heterogeneous. More sophisticated systems are needed to bring order to the complexity and allow for data to be analysed.

Stages of Data Warehouses

Data warehouses vary in how they are built, largely depending on the requirements of the ultimate output, however every data warehouse should have some key elements. The key parts of a data warehouse are:

Data Sources: This could be from internal data sources, such as daily production information or sales information, or external data sources, such as weather reports or FX rates.
Staging Area: Data is downloaded into a raw format, cleansed, divided and stored temporarily to be ready for download into storage.
Storage: Cleansed data is stored. Often data is stored in relational databases, where information is stored in specific tables which are then linked via a common field. For example, a retail business might keep store income and store size in two different tables, which can be linked together using store ID. Data is then stored in easy to access formats, such as SQL databases.
Data Marts: Data is organised by topic, e.g. sales, marketing, production information, for ease of retrieval and to help users find the information they need.
Output: Reports, dashboards, visualisations. Any sort of output that requires data. If possible, outputs can be directly linked to the Data Marts or to Storage for automated reporting and easy updating.

Infrastructure Types

There are two types of hardware used to build a data warehouse:

On-prem: Data is accessed and stored via software and hardware located on the premises of the business. E.g. you have software on your laptop to access data, data is stored in a harddrive located in the office and requests are processed by a big server located in the basement.
Cloud: Data and requests for data are transferred over the internet. The hardware which stores and processes the data can be located anywhere in the world. E.g. you use your web browser to send a request (via the internet) to access the data, the request is processed by a server in a data centre in London and the data is retrieved and sent from data stored in another data centre in Manchester.

Systems are typically set up to be either on-prem or cloud, with lots of businesses taking on IT infrastructure projects to move their systems away from on-prem to cloud. However, there is a growing trend of hybrid solutions where a mixture of on-prem and cloud is used, for reasons including cost, security and speed.

Benefits of Data Warehousing

Quality: Everyone knows what ‘messy’ data looks like. Storing and processing data in an orderly manner can increase the quality of data immensely. E.g. poor quality data might store the same customer as three separate entries due to inconsistent formatting (e.g. 1) A Nother, 2) A. Nother, 3) Nother, A). A proper data warehouse process might automatically cleanse these names and store them as one customer.
Consistency: A problem I often encounter is businesses struggling to collate data across different sources, e.g. sales data and revenue data. A typical problem is being unable to link the bookings in the CRM system to revenue, so it is very difficult to understand how sales translate to revenue and cash. A data warehouse might identify sales bookings with a unique identifier which is then consistently used across invoicing and revenue systems.
Timeliness of analysis: Many finance teams I have encountered spend 50%+ of their time preparing formulaic monthly reports, and often month-end reports are finalised halfway through the following month. A data warehouse can distill that process from weeks to hours by creating a process that automatically prepares the reports in the required format. The key benefit of this is that decisions can be made much more quickly and while the data is at its most relevant.
Volume: Regular Microsoft Excel has a maximum capacity of 1,048,576 rows. This might seem like a lot, but this is increasingly (in my opinion) becoming a limiting factor in data storage. One example is a stock broker business that required analysis on their transactional data. The data set that needed analysing was over 5 billion rows! To store and analyse that amount of data requires a proper data warehousing process.

Challenges

Cost: Creating a data warehousing system requires more infrastructure than a disorganised process. This infrastructure, e.g. cloud storage, has costs which can become substantial.
Complexity: Building a high quality data warehouse is a high skilled job and some businesses do not have employees with the right skillset to build and maintain data warehouses.
Technical debt: Poorly built data warehouses can lead to legacy issues, such as the volume of data outgrowing the data warehouse’s infrastructure. The effort to patch, upgrade or rebuild data warehouses can be problematic if they have not been built for the long term.
High Latency (slow speeds): More recently, I have seen data pipelines struggle with the volume of data being processed. For static monthly reporting (e.g. downloading a board pack), this isn’t a major issue. However, if the data warehouse is feeding a dynamic tool to make decisions in real-time, a 10 second delay to load up a new cut of data is a problem.

Summary

Data warehousing is fundamental to reporting and data analytics. Although the concepts of cleansing, organising and storing data will be fairly obvious to a lot of people, the best practices of data warehousing and how all the processes fit together are less well understood.

Data warehouses are computer systems that collect, store, process and output data. Data warehouses are often split into five stages: 1) Data sources, 2) Staging area, 3) Storage, 4) Data marts and 5) Output, although there are lots different methodologies and terminologies.

The benefits of good data warehousing are significant and, from personal experience, can transform how middle & back office teams function by reducing reporting processes from weeks to minutes. The more exciting and valuable benefit of data warehousing is that it enables in-depth and real-time analysis of businesses that facilitates faster, more accurate and more insightful decision making.

5 Comments

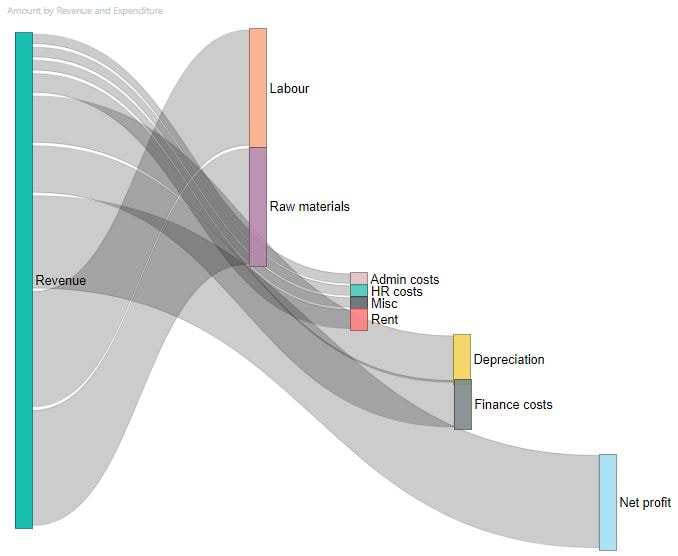
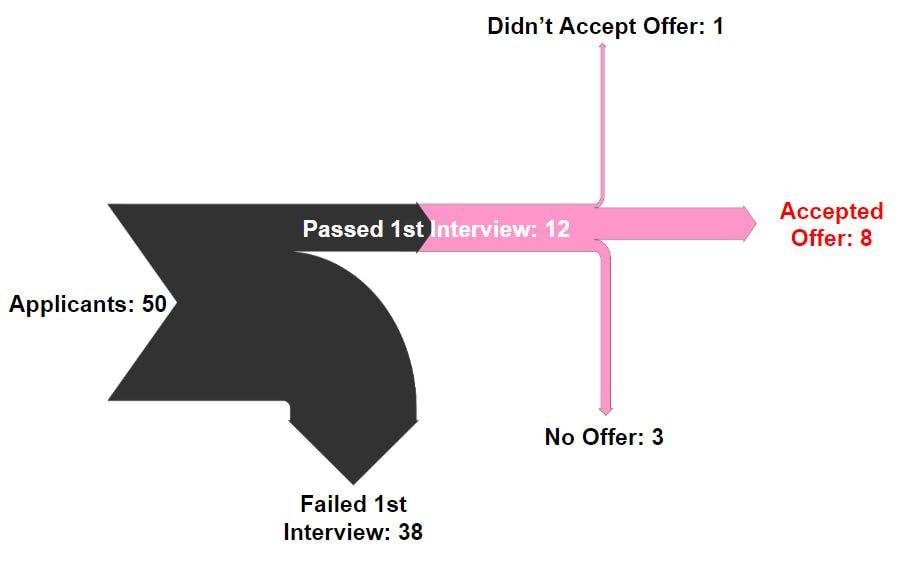
12/2/2020 2 Comments

The Sankey Diagram

Introduction

Sankey Diagrams are used to visualise flows, processes and aggregated numbers. They are especially useful when breaking down a number into its component parts. The Sankey Diagram was first used by Matthew Sankey in 1898 to illustrate the flow of energy in a steam engine system. He wanted to visualise the energy efficiency of a steam combustion system by taking the input energy and sketching out where the energy went.

Bearing in mind Newton’s first law of thermodynamics, the conservation of energy, this chart shows the energy usage in its entirety and all of the outputs of the system are equal to the input(s) to the system.

Sankey Diagrams are primarily used in physics, particularly to visualise energy systems. However, with a bit of creative thinking, Sankey Diagrams can also be used to powerfully illustrate concepts in finance and operations.

A Sankey Diagram might be helpful if you are trying to show the composition or aggregation of a number or if you are trying to link two sets of numbers which add up to the same total but are segmented differently (e.g. breakdown of costs by country and breakdown of costs by type).

Example 1: P&L Diagram

Sankey Diagrams can illustrate the breakdown of a P&L, and how revenue is ‘used’ by costs in the business to arrive at net profit. Although a slightly abstract concept, this can really help to understand the orders of magnitude of costs at different levels of a business. This chart below separates COGs, overheads and depreciation / finance costs to understand costs at the gross profit, operating profit, EBITDA and net profit levels.

An alternative diagram could show cash inflows and outflows in a business, with cash surplus on the right hand side of the diagram. If there is a cash flow deficit, this could be included on the side of cash inflows, to represent cash useage from cash reserves rather than cash inflows during the period.

Example 2: Interview Process

Processes can be tricky to visualise in an intuitive way. Sankey Diagrams can show what’s gone where during a process, which is especially useful in multi-stage processes where the inputs can go down a variety of output paths.

One example of this is an interview process, where you have a homogenous input (applicants) and a variety of output paths that the applicant can go down, from falling at the first hurdle to finally accepting an offer. With many different possible outcomes, it can be difficult to visualise the process as a whole and understand what has happened to the applicants. Sankey Diagrams are a powerful way of showing a process in its entirety and giving a sense of scale.

Summary

Sankey Diagrams are a different breed of visualisation to the standard line, bar and pie charts, and they can be used to create very intuitive diagrams. The best use cases for Sankey Diagrams are numbers that require breaking down into their component parts or visualising processes with a numerical element. The key concept to remember is that the inputs and outputs of a Sankey Diagram must be equal, similarly to Newton's law of the conservation of energy. Although these diagrams are normally used in physics and energy flow diagrams, with a little bit of creative thinking they can be applied to a much broader range of topics.

Coder’s Corner

Creating Sankey Diagrams is a bit tricky, mainly because they are not standard visualisations that are readily available in common software. I think that the easiest way to create simple Sankey Diagrams is in Microsoft Power BI (the P&L diagram was created using this software), however this software has limited customisation options for Sankey Diagrams.

If you are desperate, you can create illustrative Sankey Diagrams just using the shapes in PowerPoint or Google Slides, however the scales and sizes will probably be incorrect and creating the chart might be time consuming.

If you are more confident in Python, matplotlib includes Sankey Diagrams that can be customised and joined together. The interview process chart was created using Google Colabs with the below code. I cheated slightly by removing the labels in Python and re-including them as a text box in Google Slides, because I wanted to have text in different colours which is tricky to do in Python.

Code ->>

# Import library
import matplotlib.pyplot as plt
from matplotlib.sankey import Sankey

# Set up chart
fig = plt.figure(figsize = (40,40))
ax = fig.add_subplot(1, 1, 1, xticks=[], yticks=[], title="")
sankey = Sankey(ax=ax, scale=.05, offset=0.3, unit='')

# Stage 1 - Applicants -> Passed 1st Interview
sankey.add(flows=[50, -12, -38],
labels=['', '', ''],

# Rotate arrows for candidates leaving the process
orientations=[0, 0,-1],
trunklength = 3,
edgecolor = '#323232',
facecolor = '#323232')

# Stage 2 - Passed 1st Interview -> Outcomes
sankey.add(flows=[12, -1, -8, -3],
labels=['','', '', ''],
trunklength = 1,
pathlengths = [2,2,2,2],
orientations=[0, 1, 0, -1],

#Link Stage 1 & Stage 2
prior=0,
connect=(1, 0),
edgecolor = '#323232',
facecolor = '#ff96c9')
diagrams = sankey.finish()

# Set text size
for diagram in diagrams:
for text in diagram.texts:
text.set_fontsize(16);

2 Comments

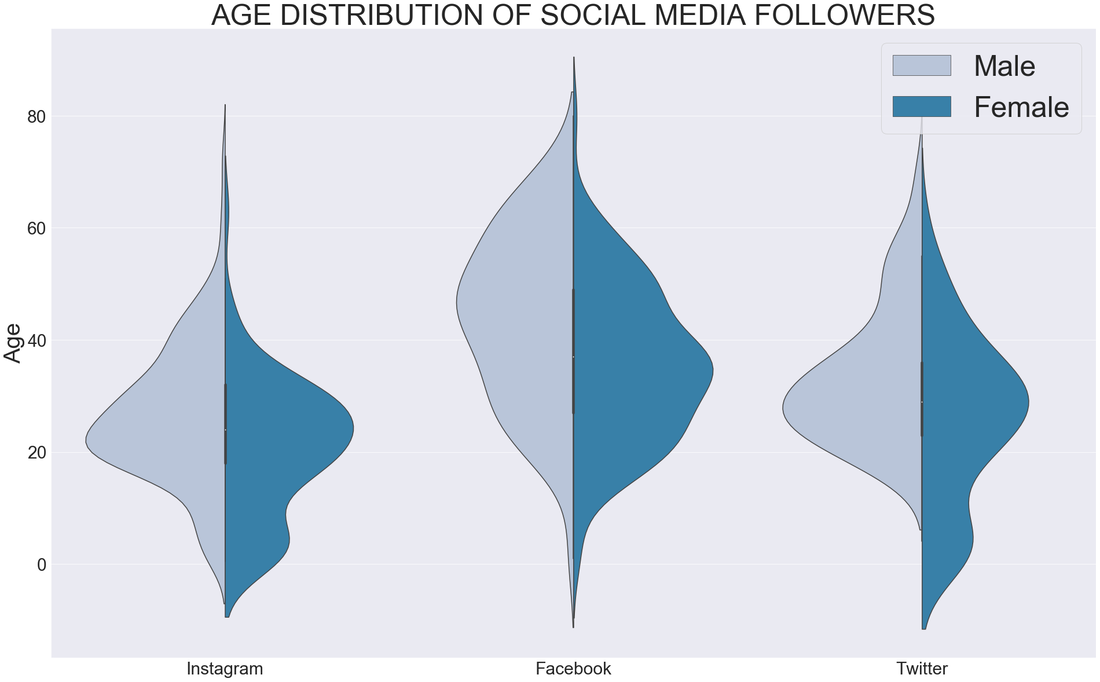
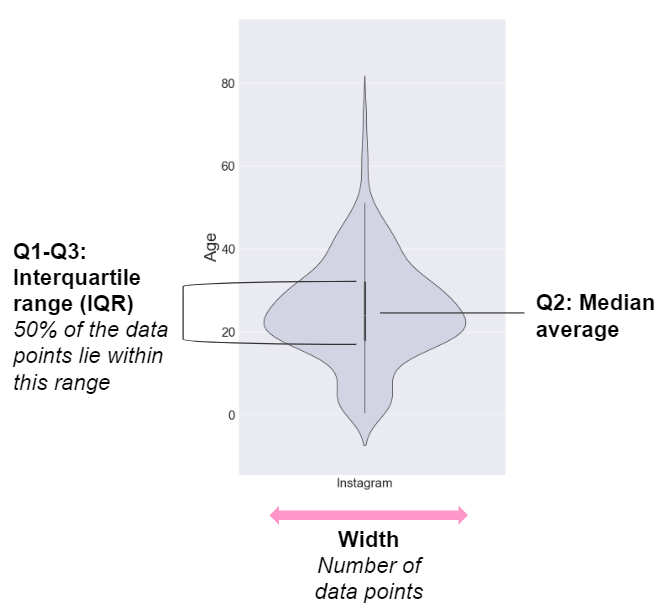
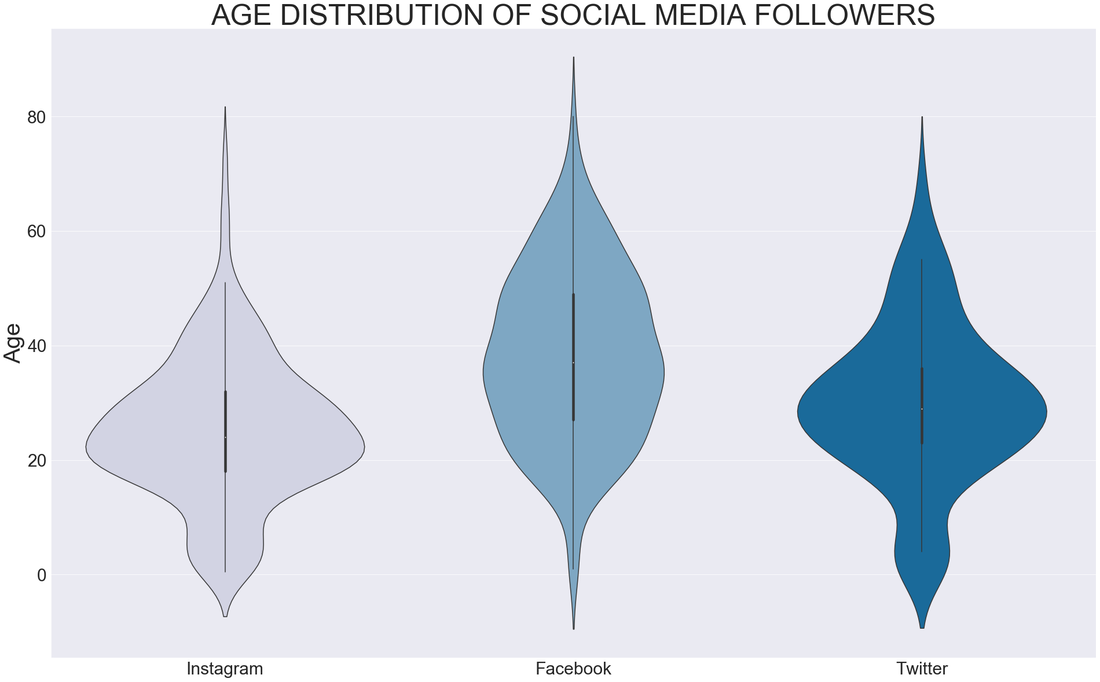
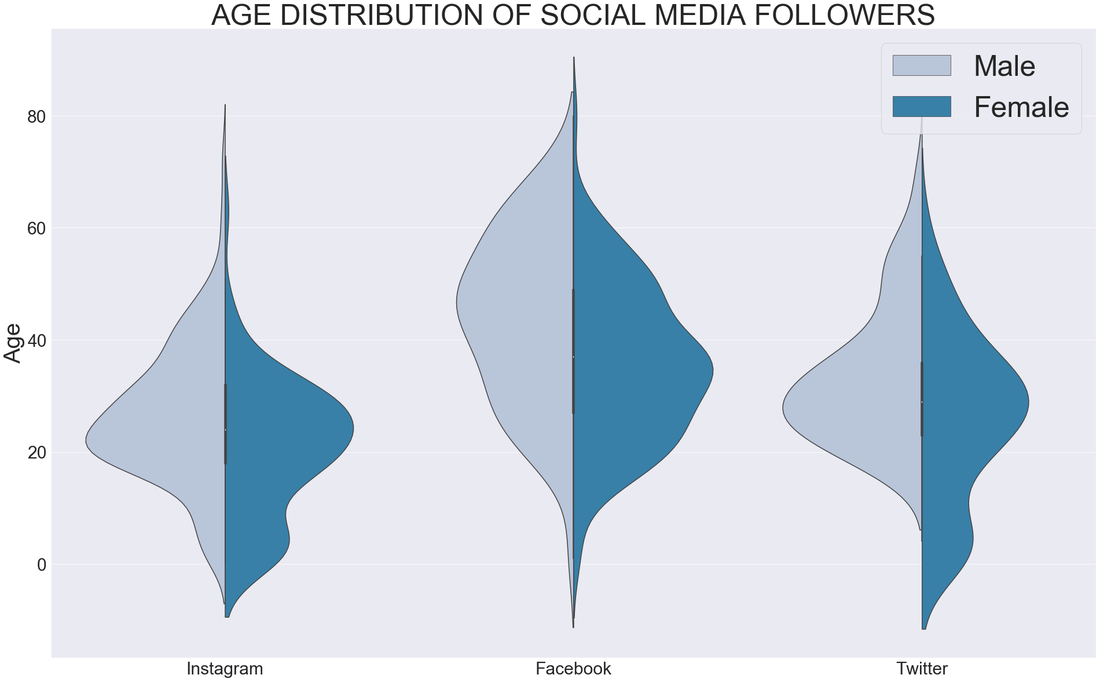
29/10/2019 2 Comments

Violin plots

Introduction

Violin plots are used to intuitively show the distribution of data in a data set. If you want to understand things like the demographics of your product users or the range of revenue per customer across different product ranges, violin plots might be the thing for you.

This article firstly covers how to interpret box plots, before setting out how to understand distribution using violin plots. Finally, it shows how to use the ‘split violin plot’ to reveal a wealth of information about a data set in a single glance.

The data used in the examples below is completely fictional and is about the social media followers of retail company. The retail company owners want to understand a bit more about the ages of their social media followers across different channels. However, they are struggling to intuitively understand the large volume of data associated with their X00,000s social media followers.

The retail company promote their brand using i) Instagram, ii) Facebook and iii) Twitter and want to optimise their content for each channel based on the age groups of their current follower base. The main questions they want to answer are:

What is the distribution of my followers for each channel?
How does that compare across channels?

Box plots

A great way to show the range of a numerical variable, such as age, is to plot the data in a box plot (also called a ‘box-and-whisker’ chart). Box plots show the distribution of a numerical variable and are useful for showing whether the data points in the data set are tightly grouped or spread out and what the range of the data set it.

This chart is most effective when different categories of things are plotted on the same chart and can be compared. In the example of the retail business who wants to understand their followers across different social media channels, they can use box plots to plot the information together and gain insights from comparing the different channels, rather than reviewing in isolation.

Violin plots

While box plots are highly effective and widely used in data analytics, they are limited in the fact that they only show specific statistical points, such as the median average or outliers, rather than the distribution of a data set as a whole.

Violin plots focus on illustrating the distribution of the entire data set and can generate different insights, that are hidden in the structure of box plots.

Although box plots are an intuitive way of understanding statistical metrics, such as interquartile range, outliers and median average, violin plots give a complete overview of a data set. Box plots are essentially summaries, meaning that the underlying distribution of the data driving the statistical metrics is obscured.

Comparatively, violin plots will give a complete overview of the distribution of data, which is especially powerful when comparing different categories within a data set, such as splitting data across seven charts to compare days of the week.

This is illustrated below, again with the example of a retail business looking to understand the ages of their social media followers. From the chart, you can quickly build intuitions about the age distributions across the channels.

Although these charts look downright weird at first, they can sometimes be a more intuitive way of understanding the distribution of data points in a data set. The two main advantages of basic violin plots are:

Clusters - Violin pots can identify unusual groups of data points. In the example above, in the Instagram channel there is a concentration of users below the Inter Quartile Range ("IQR"), users between 0-10, versus a large spread of users above the IQR, users over 30. This information is more difficult to pick out of the box plot above
Quick & powerful insights - Fundamentally, the purpose of charts is to provide insights more intuitively and more quickly than looking at raw numbers. Once you get used to them, violin plots can give a birds eye view of an entire dataset with one glance, especially when used with multiple categories for comparisons.

Next level violin plots: The Split Violin Plot

The hidden power of violin plots is that they can be split across an additional category to give an extra level of comparative analysis. This is a unique feature of violin plots and allows for particularly useful insights and, if used in the correct scenario, it can create an extremely intuitive way of explaining complicated patterns of a data set.

In the example below, the social media follower data is further split by sex of follower. As can be seen, this demonstrates the variation across category about the distribution of the ages of male and female followers. This additional split can only be used with a boolean (yes/no) variable.

Conclusion

Violin plots are very handy to have in the data visualisation toolbox. They are highly effective in showing the distribution of data points in a data set in a clear and intuitive way, and are particularly useful when used to compare different categories of data points. Violin plots can be turbocharged be being split across a yes/no variable to give even greater insight.

Coder’s corner

I made these box & violin plots using Python’s Seaborn library in a Jupyter Notebook. The code below generates the final chart (split violin plot).

You can also make violin plots in Microsoft Power BI.

2 Comments

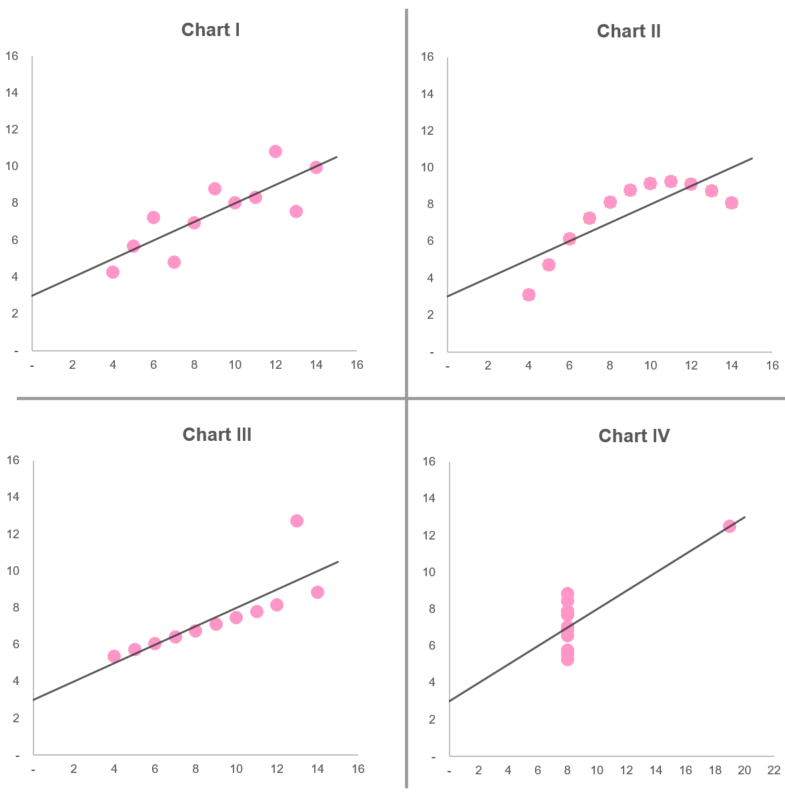
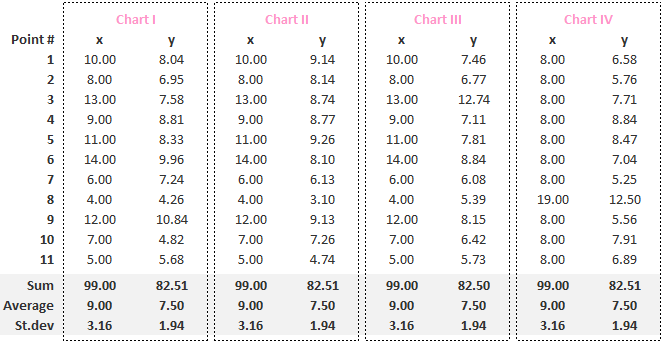
22/8/2019 2 Comments

Anscombe's Quartet

Introduction

This is a short article about an illustration called Anscombe’s Quartet. It is an extreme example of how blind statistical analysis can trick you. It is also another reminder of the importance of visualising data in your EDA (Exploratory Data Analysis).

Anscombe's Quartet

Below is a set of four distinct charts, collectively called Anscombe’s Quartet. These charts represent four different sets of data, with no obvious similarities between them. The first clue that there might be some similarities between them is that they all share similar looking trend lines, which will be explained later on.

Chart I) Evenly distributed data points showing a clear linear trend;
Chart II) Evenly distributed data points showing a clear polynomial trend;
Chart III) A clear linear trend with one outlier that looks like it is skewing the line-of-best-fit; and
Chart IV) Grouped data points along the x-axis with no trend

Even from a quick glance, it is obvious that these charts represent diverse datasets and should be understood differently. From a predictive modelling point of view, the charts indicate what sorts of analysis could be used to generate predictions about new points of data, e.g. Chart III looks like it could be modelled using linear regression and Chart IV could be a classification problem.

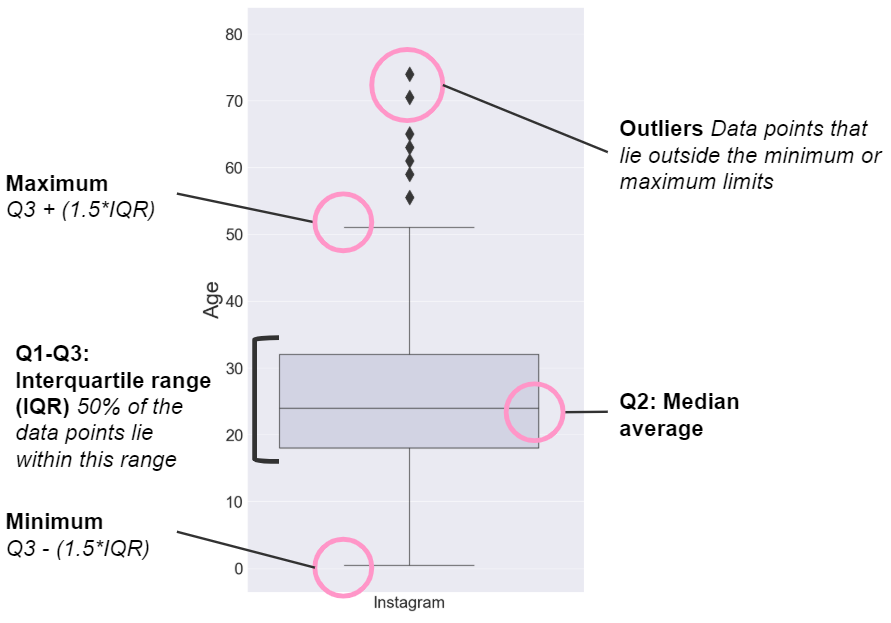
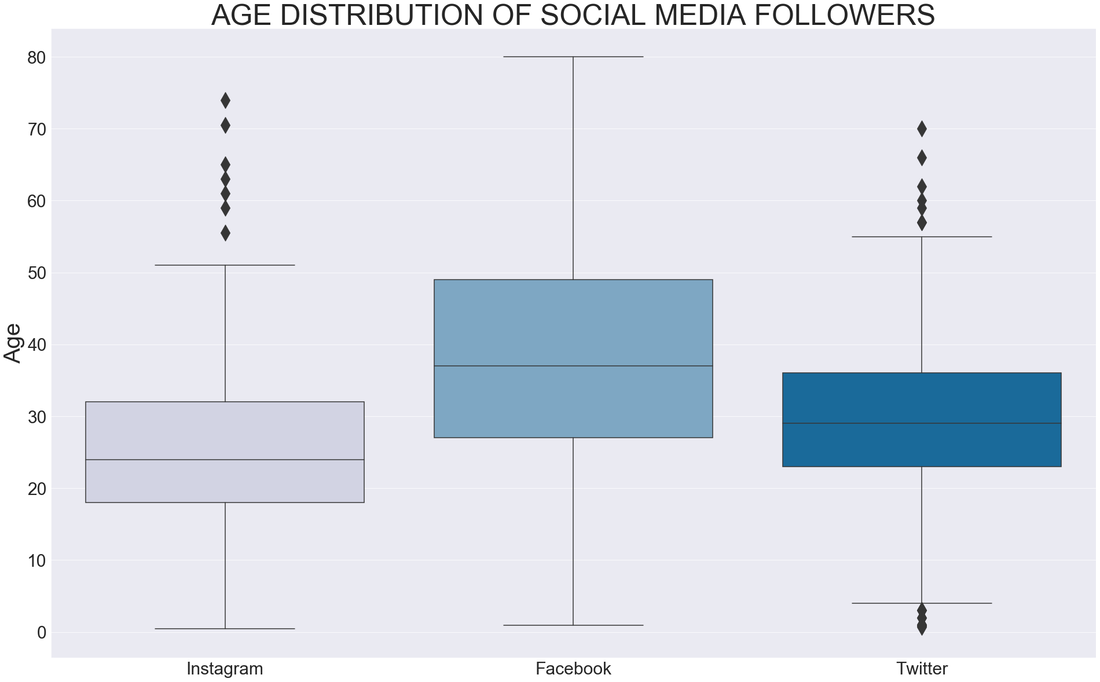
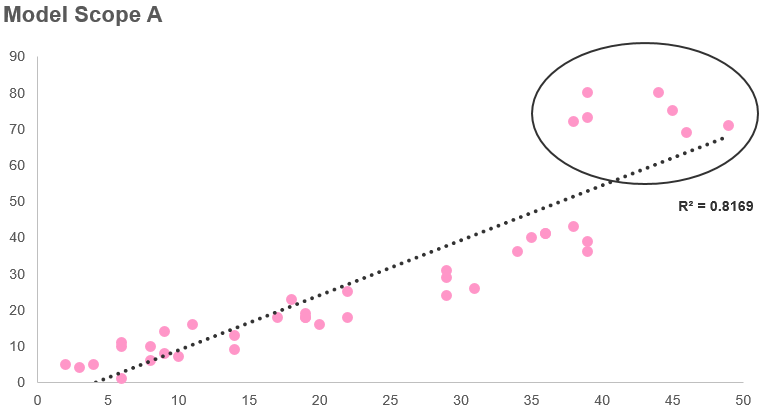
However, the statistical information about the same four charts paints a different and counterintuitive picture:

As can be seen in the table above, the Sum, Average and St.dev of the data points for each chart are identical.

So despite the fact the the data looks very diverse when visualised, each data set actually contains identical statistical properties.

Distribution

This phenomenon crops up ‘in-the-field’ very regularly, and in many different guises. The most common occurrence is when relying on averages without understanding the distribution of the underlying data, e.g. where two data sets have similar averages but wildly different distributions (in this case, the data can be visualised in a boxplot or violin plot to compare averages and distributions).

A very simple illustration of this would be measuring the average monthly revenue for two businesses, a wooly coat shop and an icecream shop. Both could have the same average monthly revenue over a year but completely different seasonal patterns.

Outliers

Another cause of this phenomenon is outliers. Outliers can skew a data set in a way that is hidden in its statistical information but obvious when the data is visualised (see Chart III above).

Although outliers could be thought of as a subcategory of distribution problems, outliers are often more subtle than looking for broader distribution patterns and need different tools to find and deal with them.

Using data visualisation, as shown in Chart III, is a solid starting point for checking for hidden outliers. However, when dealing with extremely large data sets, where the outliers might be granular and not show up in a data visualisation, another approach might be to use more complicated statistical techniques such as using z-scores.

Summary

Anscombe’s Quartet is another quick, useful reminder of why it’s important to use visualisations when exploring data and how high-level statistical information can be misleading when the data underlying those statistics is not fully understood. Remembering the message of Anscombe’s Quartet can help reduce critical errors when analysing and modelling data, where errors can be caused by a number of reasons including lack of understanding of the distribution of a dataset and outliers.

2 Comments

23/6/2019 0 Comments

Dealing with outliers

Introduction

At their best, outliers can help understand the scope and limitations of a model. At their worst, they create hidden fundamental flaws data sets that can skew models and muddy the waters of a model’s predictive power.

The method for dealing with outliers is often boiled down to ‘search and destroy’, which can lead to the loss of good data. But what if there was another way of dealing with outliers? What if you could use outliers to your advantage? What are outliers anyway?

What is an outlier

Although it is often common sense if a data point is an outlier, sometimes there are data points that lie at the margins and may or may not be outliers. In these instances, it is important to understand the essence of what outliers are and how they can be defined:

An outlier is a data point that falls outside the scope of a model or the description of a group.

For example:

a 7ft tall human is an outlier because they fall outside of our typical description of the group ‘humans’, who are almost all between 4.5ft and 6.5ft
the P/E ratio of Twitter would be an outlier for a model of P/E ratios for companies with revenue under $100m p.a., because Twitter would fall outside the scope of the model

This suggests that there is no such thing as a predetermined outlier.

A data point is an outlier depending on i) its relative characteristics compared to a group and ii) the scope of the model that is included in. If you change group or the scope of the model, a data point could cease to be an outlier.

For example:

a 7ft tall human is not an outlier because they fall inside our typical description of the group ‘mammals’
The P/E ratio of Twitter would not be an outlier for a model of P/E ratios for companies with revenue under $10b

Defining outliers is not usually this semantic, however it is important to spend time before and during analysis to think about how the definition of your outliers impacts the scope of the model and the subject matter being analysed or modelled.

How to spot outliers

By far the fastest and easiest way to spot potential outliers in a data set is through visualisation. It is best practice to visualise data in a variety of ways to spot data points that just don’t look right. Although this seems a bit unscientific to draw up some charts and assess the data by eye, it is a crucial first step in spotting potential outliers.

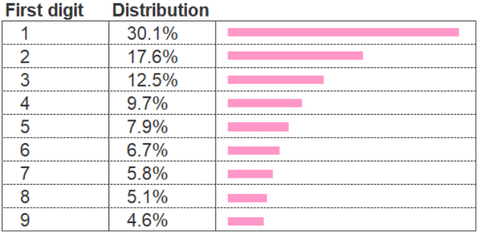
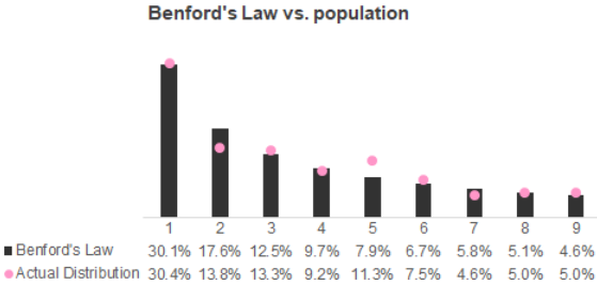
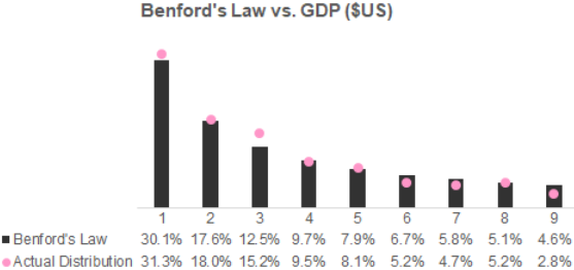
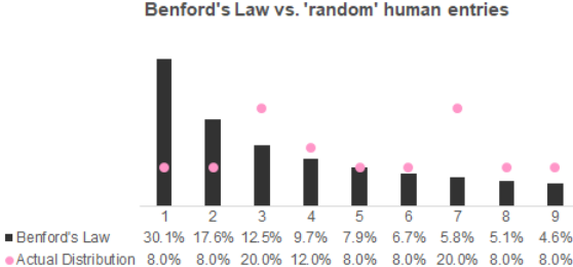
Visualisation is typically the first thing people do when trying to understand a data set. This makes a lot of sense because human beings are built to see outliers. Take a look at the picture below and think how long it took you to spot the outlier!

Solving real world problems, there is another highly effective, and sometimes more thorough, method of finding outliers; speaking to people!

In practice, data sets have owners who can reveal additional and hidden characteristics of the data set that cannot be detected through visualisation. For example, when working with a SaaS business on a customer analysis project, I asked the CFO about what they would expect to find in the data set. She told me that certain large and overseas customers have a completely different price plan than normal customers and that these customers would have a significantly lower £/employee ratio. Having this conversation meant that these customers could be excluded from the main analysis and modelled separately without skewing the general population.

Without this conversation, this information would not have been picked up by a visualisation and the model would not have taken into account the divergent price plans.

Asking questions like ‘what trends would you expect to find?’, ‘do you make any manual adjustments to the data set?’ and ‘are there any one-offs in this data?’ can help get a better understanding of a data set and help define outliers.

Dealing with outliers

Once you have defined and identified outliers, the next step is dealing with them. In general, there are three common methods of dealing with outliers:

Exclude outliers by specific instances - e.g. excluding shop x from a model of retail park footfall because you know it is closing down;
Exclude outliers by thresholds - e.g. excluding times between 2100 and 0700 when modelling retail park footfall; and
Change the scope of the model or the definition of the group you are trying to model, as outlined above.

The main disadvantage of method 1) and 2) is you sometimes exclude valuable data. For example, you are creating a model for predicting

For method 3), this is a subjective process and the pros and cons are contextual. To illustrate this, the chart below sets out some data points with some potential outliers and a linear line of best fit:

The decision is whether to a) exclude these outliers and improve the model's accuracy. These data points will be lost and the model’s breadth of predicting power will be reduced:

OR b) include the data points and change the scope of the model, which may reduce the accuracy of the model (vs. simply deleting the outliers) but will broaden the predictive power of the model:

To preserve this valuable data, there is a less commonly used fourth method for dealing with outliers: imputation.

Imputation is the method of replacing data with substitute data. Often used to fill in missing data, imputation can also be used to replace outliers. The benefit of imputation is that valuable data can be kept in the model to improve its accuracy.

With the example of modelling footfall in a retail park, if one of the shops were closed for refurbishment 3 months of the year it would be an outlier. An easy way to prevent this outlier from skewing the data set would be to exclude it. An alternative approach could be to impute data from the same 3 months of the previous year, +/- a growth rate. This way you could retain the 9 good months and have a fair substitute for the outlier 3 months.

Summary

At their best Outliers are subjective and depend on i) the definition of the group that the data point belongs to and ii) the scope of the model that the data points are being used in.

The quickest way of spotting outliers is through visualisation and looking at which data points stand out or if there are any unusual visual patterns in the data. Speaking to people is another effective way of finding outliers, and can even identify hidden outliers that could not be found by analytically or visually interrogating the data.

Dealing with outliers can be very straightforward, e.g. simply deleting the outlier, or more complicated if using imputation to substitute the outlier using other data.

0 Comments

26/4/2019 2 Comments

Benford's law

Introduction

If you picked a random country and measured its population, there’s roughly a 30.1% chance the first digit of that number is a ‘1’ and a 17.6% chance that it is a ‘2’. The distribution of these first digits is known as Benford’s Law.

Benford’s Law, also known as the ‘leading digit rule’, appears everywhere in economics, human geography, nature and sports, but few people have ever heard of it.

Why does this mathematical phenomenon exist? Where does it appear? So what?

What is Benford’s Law?

Think of all the numerical data that you have created over the last 7 days: bank transactions, journey times, journey distances, doorways walked through, milliliters of water drunk, how many words you’ve spoken.

For each of these numbers, Benford’s Law says that the likelihood of the first digit being a ‘1’ is not 11.1% (1/9), but is in fact around 30.1%. Benford’s Law sets out a distribution curve of leading digits, with ‘1’ being the most likely and ‘9’ being the least likely, as follows:

This distribution has been found to occur in a spooky amount of datasets. For example, below is the distribution of leading digits for the population of 240 countries. Although there are small divergences from Benford’s Law, the pattern is clear:

Here is the same analysis using annual GDP(US$):

When does this rule work?

Fully explaining why this phenomenon occurs is at the difficult difficult lemon difficult end of mathematics.

However, in general the rule will work with most statistical data which spans several orders of magnitude, e.g. 10^1-4.

Counter-intuitively, it’s probably easiest to understand the conditions where the distribution won’t be found:

Sequential numbers: Any sets of numbers which form a consecutive or formulaic pattern will not work, e.g. invoice numbers, dates. This is because these data sets can, and probably will, have arbitrary cut-offs, starting points, end-points. There is no reason why a list of invoice numbers can’t start at ‘2...’ or ‘3...’ or always start with a ‘2002...’
Max/min conditions: If the number set has limits and thresholds it can skew the distribution. For example, if you asked people to ‘pick a number between 150-550’, you would not get a Benford’s Law distribution
Artificial clusters: Sometimes humans like to make their life easy and measure things with convenient scales. Take human height as an example. The average UK woman is 162 cm tall, with very few being under 100cm or over 199cm and none being over 299cm
Human bias: Data created by human decision making can carry inherent biases. For example, humans are influenced by price thresholds when making purchasing decisions, which is why many prices are £x.99. This is also true when humans pick ‘random’ numbers, where people will disproportionately choose 3 or 7 when picking a number between 1-10
‘Building block’ numbers: Some recorded numbers are the result of combining other numbers. If you were looking at the distribution of leading digits of bets in a poker competition, the results might not follow a Benford’s Law distribution because each bet is built up from fixed chip values. If the smallest chip size is $25, bets of $10, $20 and $30 would be impossible. Another example might be a fast food restaurant with a small menu, where there are relatively few combinations of items that can form a transaction value.

How can I use Benford’s Law?

When it was initially discovered in the 19th century and rediscovered in the mid-20th century, Benford’s Law was filed away under ‘interesting but not useful’. In the pre-computer era, data collection and analysis was slow and painful.

Today, it is extremely straightforward to check whether a dataset has a Benford’s Law distribution of leading digits. I think that Benford’s Law is an incredibly useful tool that can quickly help you understand the characteristics of a data set and identify hidden biases.

The most common uses of Benford’s Law in data and analytics are:

Fraud: Benford’s Law became fashionable again when people realised its use in fraud detection. This follows from the human bias point made above where humans will make strange decisions when choosing ‘random’ numbers.

When I was in forensic accounting, we used Benford’s Law to sense check accounting software entries. If large numbers of transactions had been entered ‘randomly’ by a human there would be a distinct divergence away from a Benford’s Law distribution.

This is an example of what the leading digit distribution pattern of a human entered dataset might look like versus Benford’s Law:

Bias: This is the most useful application of Benford’s Law. It can help detect hidden biases in a data set, possibly caused by some of the conditions outlined above under which Benford’s Law won’t work.

This is incredibly useful for data analysis and creating machine learning models because it helps remove unidentified biases from datasets that can lead to a misleading, at best, or fundamentally flawed models.

For example, you take a dataset of credit card transactions and compare the leading digit distribution to Benford’s Law. The analysis shows that there is a higher than expected proportion of ‘5’s and ‘6’s as the leading digit of the transactions. On further investigation, you find out that in December 2018 the credit card company ran a promotion for transactions on electronic goods of £500 or above. These transactions are excluded from the model where appropriate.

Summary

Benford’s Law, or the ‘leading digit rule’, is a solid combination of being interesting and useful. It's also much more applicable than given credit for.

Not only is it a quick and high level data exploration tool which can help understand a dataset, it can be a robust forensic technique that can be and has been used as legal evidence.

Understanding the characteristics of datasets under which Benson’s Law won’t work is the key to applying and using it in data and analytics.

2 Comments

YOUR CART

ARTICLES

data warehousing

The Sankey Diagram

Violin plots

Anscombe's Quartet

Dealing with outliers

Benford's law

Author

Archives

Categories

Sign up for more LONDONSODA